Tarea 18 Visualización de Matemáticas

Después de mucho buscar, no he encontrado ningún experimento de matemáticas expuesto en algún museo, que no haya sido puesto ya , pero he encontrado trucos de magia con matemáticas que al fin y al cabo es una forma divertida de incluirlas en nuestra vida y a la vez así, demostrar ciertas reglas matemáticas. Aquí os dejo la dirección: http://www.juegosdelogica.com/neuronas/matemagi.htm

Tarea 18 Visualización de las matemáticas

Aquí un vídeo donde se relacionan las ecuaciones diferenciales con el movimiento armónico simple, cosa esta que nos ayuda a entender mediante imagines y sistemas reales, tangibles  como "el angulo de un péndulo, o la rotación de una cuerda de reloj"  una de las funciones que desempeñan las derivadas en la vida cotidiana.

ENLACE: http://www.youtube.com/watch?v=t_5f3WbUfrw

Preguntas 2º parcial

1º Un problema a resolver con ecuaciones diferenciales

2º Un ajuste lineal o exponencial

3º Un volumen de revolución  (para hacer por integrales)

4º Métodos numéricos

5º   Discutir un sistema dependiendo de parámetros a y b.

6º  Una pregunta de números complejos con 4 apartados.

Tarea 18

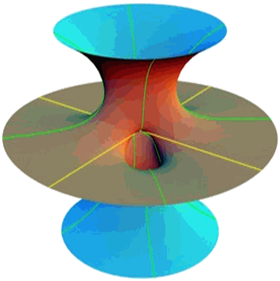Este es un experimento realizado por la Facultad de Ciencias de Granada para entender y relacionar la geometía con las formas obtenidas en el experimento.

 "A partir de una serie de experimentos realizados con distintas estructuras de alambre introducidos en agua jabonosa, vamos planteando cuestiones geométricas sencillas de entender como el problema isoperimétrico o el de hallar superficies con área mínima.

  Las diferentes formas geométricas producidas son superficies visualmente atractivas que encierran problemas matemáticos más profundos. El objetivo del taller es aproximarnos a estos objetos geométricos y a llegar entender las matemáticas que llevan aparejados."


http://fciencias.ugr.es/index.php?option=com_content&view=article&id=1099%3A27-experimentos-con-pompas-de-jabon-2012&catid=20&Itemid=115&lang=es

TAREA 18

La Máquina de Galton: Curva de Gauss

                 UAZ SIGLO XXI
 (El Museo de Matemáticas, un lugar para
pensar, reflexionar y aprender jugando)

 

Un experimento o mejor dicho experiencia es el denominado Aparato de Galton, quevisualiza el perfil de la curva de Gauss.Actualment lo podemos encontrar en el museo UAZ SIGLO XXI en México. 

 

 

 

 

 http://www.youtube.com/watch?v=5_HVBhwhwV8

 

 

 

 

 

Museo matemático

Aprovechando que había que realizar esta tarea, he podido topezarme con un portal, al cual todos podeis acceder a el, (aunque está en inglés).
Se trata de un museo de las matemáticas que se va a inagurar el proximo 18 de Diciembre en Manhattan. No importa donde se encuentre, pero lo que más me ha llamado la atención es que va dedicado sobre todo para los más peques de la casa. Para que puedan jugar y sobrevalorar más facilmente a primera mano las "matemáticas" que tanto nosotros como ellos, tenemos en nuestra vida diaria.  

También tienen monitores, los cuales les explican con ejemplos el sentido de las matemáticas con la vida. Como es muy reciente en la web, no se puede ver que secciones tiene o tendrá el museo, pero en la seccion de Galeria de fotos, se pueden encontrar muchos temas, uno de ellos son eclipses 

creadas con combas o como se observa en la imagen superior, los niños recorren una circunferencia a través de unos carriles siempre en el mismo sentido, para poner ejemplo los satélites geostacionarios sobre la tierra o el sol con la tierra...

Fuente: Ir

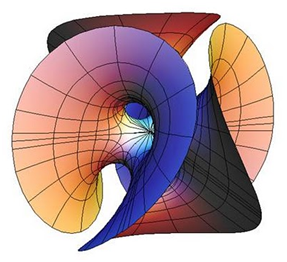
Tarea 18: Máquina de Generación Rotante de Hiperboloide.

En el museo de la universidad de Buenos Aires podemos encontrar distintas exposiciones sobre las matemáticas, una de ellas es ésta: Máquina de Generación(Rotante de Hiperboloide).
Explicación del modelo:
 Consta de dos segmentos de recta alabeados que giran entre sí (barras). El móvil genera un hiperboloide circular y pasa por una ranura de forma hiperbólica que corresponde al corte del hiperboloide con un plano vertical. Se acompaña a ésto por algunas reglas fijas de un hiperboloide un poco mayor.

ANIMACIÓN:

Aquí os dejo el enlace para quien este interesado en ver las distintas exposiciones, hay algunas muy interesantes como el modelo trazador de la elipse o el de la parabola...

http://mate.dm.uba.ar/~lechague/modelos.htm

TAREA 18:
                            
               VISUALIZACIÓN DE LAS MATEMÁTICAS

Estos son algunos programillas educativos que nos pueden ayudar a  visualizar varios conceptos en matemáticas, física, y la ingeniería. 

Pueden verlos con cualquier navegador Java.

Aqui dejo el enlace:

               http://www.falstad.com/mathphysics.html

tarea 18 mmaca

http://www.mmaca.cat/

En esta página podemos ver un museo de matemáticas donde se exponen varios talleres de matemáticas muy interesantes como el del cicloide como vimos en la visita al mudic y algunos mas como el de la parábola que describe el agua

MUDIC

El día sábado 24 de noviembre visité el Mudic, donde nos explicaron de manera visual conceptos de las matemáticas tales como la elipse, la curva cicloide o el teorema de pitágoras.

Lo que más me llamó la atención fue la mesa de billar donde explicaban la geometría de esta curva, sus focos, la distancia que hay desde el perímetro hasta ellos y además de nos contaron ejemplos que podemos ver en la naturaleza, como que muchas especies de aves fabrican sus nidos con forma de elipse, ya que por tener dos focos, y no sólo uno como el que tiene una circunferencia, distribuye mejor el calor y de esta manera los huevos que haya en el nido están a la misma temperatura unos de otros.

Esta es la forma que tiene una elipse:






Y esta es una foto de la mesa de billar elíptica del Mudic:

A los que nos pudistéis ir ese día os lo recomiendo, los chicos que nos guiaron durante la visita fueron muy amables y nos lo pasamos muy bien!!!

TAREA 18-visualización de las matemáticas

Entre los módulos de este museo, podemos encontrar la Máquina de Poleas, Bielas y Levas.
Su relación con las matemáticas trata de las Coordenadas polares, Derivada polar, Longitud de arco, Pendiente polar y la Tangente a una curva cerrada. aqui dejo el enlace http://www.fcen.uba.ar/museomat/bielas.htm

TAREA 18: VISUALIZACIÓN DE LAS MATEMÁTICAS

En el departamento de matemáticas de la universidad de  Buenos Aires, han creado un museo interactivo de las matemáticas en el que se muestran diferentes maquinarias que sirven para la visualización de las matematicas en el mundo real. Un ejemplo de ello en el Billar Elíptico o la maquina de integrar.

Aquí dejo el enlace general desde donde se puede acceder a las diferentes maquinarias de estudio de las matemáticas.

http://www.fcen.uba.ar/museomat/maquinas.htm

Tarea 18: Multiplicar sin calculadora.

En el siguiente vídeo presento un modo rápido de multiplicar números enteros bastante curioso. En caso de que la calculadora quede sin pilas o se nos olvide, ya tenemos solución.

TAREA18: Museo de las ciencias.

En el museo de las ciencias de la Universidad Nacional Autónoma de México encontramos distintas exposiciones relaciones con las matemáticas: Geometría clásica, Poliedros, Caleidoscopios,  Galería de números, Probabilidad, etc...

En la sección de Galería de números encontramos los números racionales, irracionales, negativos y los imaginarios. Esta exposición guarda relación con parte del temario impartido en la asignatura de matemáticas.

Aquí os dejo el enlace del museo: http://www.universum.unam.mx/expo_matematicas.php

TAREA 18: MAQUINA DE INTEGRAR.

En el enlace que dejaré a continuacion de la universidad de buenos aires se nos presenta una máquina cuya funcion es la resolución de integrales, tema visto en clase, en dicha pagina se nos hace una breve introduccion de la máquina y de su funcionamiento.
http://www.fcen.uba.ar/museomat/integra.htm

La Cicloide

http://revmat.webs.ull.es/geometria/cicloides/ciclon.htm

Éste es un enlace que os llevará en una página donde podemos ver bastante información sobre la cicloide,ya que la visitamos el museo ''MUDIC'' y nos hicieron una pequeña demostración en la que vimos que soltando las dos bolas en el mismo tiempo,pero a la distancia que nosotros queramos,las dos bolas siempre chocaban en el mismo punto.

Fermer

http://translate.google.es/translate?hl=es&sl=bg&u=http://www.fermer.bg/&prev=/search%3Fq%3Dfermer.bg%26hl%3Des%26tbo%3Dd%26biw%3D1440%26bih%3D717&sa=X&ei=Me-9UMyPL8Oc0QXE3oDoCA&sqi=2&ved=0CDMQ7gEwAA


Por lo que podemos ver en el siguiente enlace,se trata de las noticias sobre todo lo relacionado de la agricultura,es decir, la página ''fermer.bg'' es de gran importancia ya que nos informa de las exportaciones e importaciones hacia otros países;los precios de los productos,tal como la subida y bajada de estos mismos,y finalmente,una pequeña información sobre la maquinaria agrícola que nos puede servir como orientación de cómo cultivar un determinado producto.

Libro para el maestro

http://www.reformasecundaria.sep.gob.mx/matematicas/pdf/orientaciones/libromaestro.pdf


El siguiente libro ''Libro para el maestro'',es un libro de matematicas es muy importante,ya que en él,podemos encontrar capítulos y ejercicios de secundaria que estamos viendo en las clases de matemáticas,especialmente el tema de álgebra,ecuaciones lineales,máximos y mínimos,que los podemos ver en las páginas 125 hasta la 180.

COMO MEDIR EL NUMERO pi

                             

Apartir del Número Aureo

1,618033988749894848204 La sección áurea, en matemáticas, es una proporción de la geometría que se obtiene al dividir un segmento en dos partes de manera que el cociente entre la longitud del segmento mayor y la longitud del segmento inicial es igual al cociente entre la longitud del segmento menor y la del segmento mayor.
El punto C crea una sección áurea en el segmento rectilíneo AB si AC/AB = CB/AC. Esta proporción tiene el valor numérico 0,618..., que se puede calcular de la siguiente manera: si AB = 1 y la longitud de AC = x, entonces AC/AB = CB/AC se convierte en x/1 = (1 - x)/x. Multiplicando ambos lados de esta ecuación por x, se tiene que x2 = 1 - x; y por tanto x2 + x - 1 = 0. Esta ecuación de segundo grado se puede resolver utilizando la fórmula cuadrática, que da x = (-1 + Ä)/2 = 0,6180339...
Ciertos historiadores afirman que las propiedades de las secciones áureas ayudaron a los discípulos del matemático y filósofo griego Pitágoras a descubrir las rectas inconmensurables, que son el equivalente geométrico de los números irracionales. Sin embargo, lo que sí es cierto es que desde la antigüedad, muchos filósofos, artistas y matemáticos se han interesado por la sección áurea, que los escritores del renacimiento llamaron proporción divina.
Leonardo Da Vinci hizo las ilustraciones para una disertación publicada por Luca Pacioli en 1509 titulada De Divina Proportione , quizás la referencia más temprana en la literatura a otro de sus nombres, el de "Divina Proporción". Este libro contiene los dibujos hechos por Leonardo da Vinci de los cinco sólidos platónicos. Es probable que fuera Leonardo quien diera por primera vez el nombre de sectio áurea . En 1525, Alberto Durero publica Instrucción sobre la medida con regla y compás de figuras planas y sólidas donde describe cómo trazar con regla y compás la espiral basada en la sección áurea, que se conoce como "espiral de Durero".

Material Necesario

Una tira de papel, una regla, un objeto cilíndrico, por ejemplo, una lata de refresco.

Método

• Rodea la lata con la tira de papel y corta lo que te sobre o haz una marca en la tira.
• Sitúa la tira sobre una superficie horizontal y mide su longitud o hasta la marca si decidiste no cortar la tira.
• Mide el diámetro de la lata. Puedes situarla entre dos objetos y luego medir la distancia entre ellos.
• El cociente entre las dos medidas es el número .

Explicación

La relación entre la longitud de una circunferencia de radio r (2r) y su diametro (2r) es

TAREA 18: mmaca

En el Museu de Matemàtiques de Catalunya, he encontrado un módulo muy interesante sobre azar. 

En los enlaces que pongo a continuación se explica el módulo y como los jóvenes que visitan el  museo pueden realizar la actividad en el mismo.

http://www.mmaca.cat

http://phobos.xtec.cat/creamat/mmaca/images/imatges/moduls/atzar_no_regular/atzarnoreg.pdf

Tarea nº 18: Visualización de Matemáticas

Aquí os dejo el enlace de un módulo de matemáticas bastante interesante sobre el billar elíptico. http://www.fcen.uba.ar/museomat/billar.htm

TAREA 18.SALAS DEL MUSEO VIRTUAL DE LA CIENCIA

SALA DE LA MEDIDA

El lenguaje empleado en la metrología desde la antigüedad, con más o menos precisión, ha sido el que ahora reconocemos como matemático, a lo largo de siete artículos podremos comprender como la humanidad ha ido estableciendo distintas unidades de medida y patrones para poder comprender mejor el mundo que le rodea. De un modo ameno, Don Metro, nos guiará durante este proceso histórico. Enlace: http://museovirtual.csic.es/medida/med.htm

Tarea 18: La visualización de las matemáticas

El carril de aire, objeto utilizado en la experiencia de analizar un MRU o un MRUA desde el punto de vista energético y su relación con los análisis cinemático y dinámico (segunda ley de Newton) recoge la utilización de las integrales, como explicaré a continuación:

Las integrales fueron utilizadas por Newton para determinar la relación que existía entre la velocidad, el tiempo y el espacio recorrido, de aquí, la famosa ecuación V=e/t. Pero todo esto solo funciona si la velocidad es constante, si no lo es, necesitamos utilizar las integrales.

Si sabemos como varía la velocidad con respecto al tiempo podemos calcular el espacio recorrido y viceversa. En resumen, necesitamos saber las variaciones de 2 incógnitas para resolver la ecuación.

Os dejo una explicación más detallada y adjunto foto del carril de aire:

Enlace: http://www.sc.ehu.es/sbweb/fisica/cinematica/rectilineo/rectilineo.htm

Carril de aire:

Para tomar las variaciones del tiempo, el carril, consta de 2 sensores que captan un intervalo, el tiempo del intervalo depende del angulo que forma con la horizontal y el espacio será la distancia entre los intervalos.

 TAREA 18

El Museo de las Ciencias de Londres consiguió construir una máquina diferencial Nº 2 totalmente funcional,
siguiendo los dibujos y especificaciones de Babbage.

http://www.analisisinformaticoscft.blogspot.com.es/2012_08_01_archive.html

Tarea 18.

Entre los módulos de este museo, podemos encontrar "la máquina de engranajes"; donde su relación con las matemáticas son: las coordenadas polares, la derivada angular, longitud de arco y pendiente polar.
Y, donde podemos observa que una de la relaciones que tiene, las derivadas, las hemos explicando y trabajado en clase.

http://www.fcen.uba.ar/museomat/engranaj.htm