sábado, 6 de octubre de 2012
Geometría en los copos de nieve
Geometría en los copos de nieve
En 1611 un
señor llamado Johannes Kepler se percató de la curiosa geometría en los copos
de nieve. A partir de ahí, realizó un estudio basado en los copos de nieve y la
geometría hexagonal. Aunque también se pueden llegar a formar copos de nieve
cuya geometría esta basada en el triángulo o en el decágono, dependiendo de la
temperatura y la humedad a la que se hayan
formado.
Wilson Alwyn
Bentley estudió la geometría de diversos copos de nieve fotografiándolos al
microscopio, sin embargo no puedo encontrar dos copos de nieve idénticos, por
lo que planteo la teoría de que no podían existir dos copos iguales.
Más tarde, hacia el 1988, un equipo en Wisconsin pudo verificar que dos
copos de nieve sí que podían ser idénticos, si se formaban en un ambiente muy
parecido. Además, autentificaron dicha
afirmación con un
experimento, en el cual se demostró que existían copos de nieve iguales, aunque
estos se correspondían con prismas huecos y no con los copos comúnmente
conocidos.
A continuación
se pueden observar diversas geometrías
en copos:
Cristales dodecagonales
Láminas sectoriales
http://recuerdosdepandora.com/ciencia/matematicas/geometria-de-los-copos-de-nieve/
![\int_3^7\frac{2x+x^2+x^3}{\sqrt[5]{\tan{x}}+3x^2\frac{x}{3x^5}}](http://rinconmatematico.com/latexrender/pictures/22eeb81931dfbe40c34f220206e6c2bc.gif "\int_3^7\frac{2x+x^2+x^3}{\sqrt[5]{\tan{x}}+3x^2\frac{x}{3x^5}}")
Las ondas desde un punto de vista matemático
Las ondas nos son muy conocidas por el océano, por el estudio del sonido, por los terremotos y por otros fenómenos naturales. Para entender a las ondas, necesitamos entender las medidas asociadas a ellas, como su frecuencia, su longitud y su tamaño vertical. Para lograr predecir el comportamiento, podemos ver las ondas usando una fórmula matemática, ya que la forma de una onda se repite a intervalos constantes a lo largo del tiempo y la distancia.
Los matemáticos usan la función seno (Sin) para expresar la forma de una onda. La ecuación matemática que representa la onda más simple es la siguiente:y = Seno(x) .
Para poder representar otras formas de ondas, especialmente aquellas que son más largas o más grandes necesitamos añadir otros términos a nuestra fórmula: y = ASeno(x) ,A nos da el valor de la amplitud de la onda.Para modificar la longitud de onda de una onda,se usa el modificador k, como se puede ver en la fórmula siguiente: y = ASin(k*x). k extiende la longitud de la onda.
Si trazamos el seno de un ángulo medido en radianes en el sistema de coordenadas cartesiano, obtenemos la característica subida y bajada. La medida del ángulo está trazada a lo largo del eje x, la gráfica que se obtiene es una curva continua que se parece a una onda física.
Los matemáticos usan la función seno (Sin) para expresar la forma de una onda. La ecuación matemática que representa la onda más simple es la siguiente:y = Seno(x) .
Para poder representar otras formas de ondas, especialmente aquellas que son más largas o más grandes necesitamos añadir otros términos a nuestra fórmula: y = ASeno(x) ,A nos da el valor de la amplitud de la onda.Para modificar la longitud de onda de una onda,se usa el modificador k, como se puede ver en la fórmula siguiente: y = ASin(k*x). k extiende la longitud de la onda.
Si trazamos el seno de un ángulo medido en radianes en el sistema de coordenadas cartesiano, obtenemos la característica subida y bajada. La medida del ángulo está trazada a lo largo del eje x, la gráfica que se obtiene es una curva continua que se parece a una onda física.
 * |
La onda más sencilla es la onda sinusoidal descrita por la función: 
Donde
es la amplitud de una onda y las unidades de amplitud dependen del tipo de onda
Las olas del mar son ondas sísmicas superficiales. Se trata de un vaivén con una componente vertical, de arriba a abajo, y otro longitudinal, la dirección de propagación de la onda. El fenómeno es provocado por el viento, dando lugar primero a arrugas en la superficie del agua, llamadas ondas, el efecto de fricción se intensifica y las pequeñas “arrugas” iniciales dejan paso a olas de gravedad.
Donde
es la amplitud de una onda y las unidades de amplitud dependen del tipo de ondaLas olas del mar son ondas sísmicas superficiales. Se trata de un vaivén con una componente vertical, de arriba a abajo, y otro longitudinal, la dirección de propagación de la onda. El fenómeno es provocado por el viento, dando lugar primero a arrugas en la superficie del agua, llamadas ondas, el efecto de fricción se intensifica y las pequeñas “arrugas” iniciales dejan paso a olas de gravedad.
Entender las matemáticas de las funciones de las ondas, nos permite entender mejor el mundo natural que nos rodea. Las diferencias entre los colores que se ven en esta página, tienen que ver con las diferentes longitudes de ondas percibidas por nuestros ojos. De la misma forma, la diferencia entre el trinar de un pájaro y el estruendo de una locomotora se debe al tamaño de las ondas de sonido que se emiten. Las ondas, y por consiguiente las ondas matemáticas, nos rodean constantemente.
Bibliografía: wikipedia, http://www.visionlearning.com/library/module_viewer.php?mid=131&l=s
![\int_9^3\sqrt[3]{9}\frac{5}{6
}](http://rinconmatematico.com/latexrender/pictures/4f34ccdec8f53965f164acb93b2dd169.gif "\int_9^3\sqrt[3]{9}\frac{5}{6
}")
![\int_42^8 \frac{20}{12}\sqrt[3]{3}](http://rinconmatematico.com/latexrender/pictures/355093a4ded598950b72eb054d57f11e.gif "\int_42^8 \frac{20}{12}\sqrt[3]{3}")
viernes, 5 de octubre de 2012
![\int_2^3\frac{\sqrt[3]{4x}cosx}{2x}dx](http://rinconmatematico.com/latexrender/pictures/dbe26d34744c3f5e71194307a24e1611.gif)
La naturaleza son matemáticas.
Tanto en los animales y como en las plantas podemos
encontrarnos algunas coincidencias curiosas, cabe destacar entre otras, el
número de semillas de una espiral de un girasol y los pétalos de muchas flores,
que siguen el mismo patrón que el caparazón de un caracol, donde nos encontramos con los números de Fibonacci.
La forma en que se ordenan las semillas en el girasol, si cuentas bien los
espirales que se forman hacia la derecha y hacia la izquierda, verás que hay 34
curvas en un sentido y 21 en el otro: ambos son números consecutivos de la
sucesión de Fibonacci.
También podremos observar los números de Fibonacci en el estudio
de poblaciones idealizadas de conejos (el ejemplo inicial que usó Fibonacci),
así como en vacas y abejas; en el número de espirales que forman los granos de
frutos como las piñas de pino o en el ordenamiento de las hojas en una rama
para obtener de manera más efectiva la forma de organizar las estructuras. Ese patrón permite, entre otras cosas, que las ramas
crezcan sin hacerse sombra las unas a las otras.
La razón por la que los números de Fibonacci pueden encontrarse en
tantos ejemplos de la naturaleza, se relaciona estrechamente con el nexo que
existe entre esta sucesión y el número áureo que es igual a 1.168.
Esta relación,
aunque parezca mentira, no es causal, sino que responde a una serie de fórmulas
matemáticas que aparecen una y otra vez en un gran número de seres vivos.
Si analizamos el número áureo y la serie de
Fibonacci, su desarrollo puede ser
complicado de entender, pero podemos descubrirlos de manera natural. Para que
lo entiendas, nadie calcula si la distancia entre la nariz y el mentón es
proporcional a la longitud total de la cara, pero si es así, consideramos a esa
persona bella.
El empaquetado en espiral de proporciones áureas aparece a su vez en las hojas de los aucauciles o en las
estructuras de una piña. En
ellas también encontramos la serie de Fibonacci: el número de hojas de una
espiral de aucaucil siempre pertenece a este sistema; el de la espiral
contraria es el número anterior o superior de la serie.
Fibonacci creó su famosa serie al intentar descubrir cómo mejorar la cría de conejos.
La secuencia relaciona el número de nacimientos que tienen lugar cada período
de cría, comenzando con los números cero y uno, denominados generadores. A
partir de ahí los siguientes números son la suma de los dos anteriores: 0, 1,
1, 2, 3, 5, 8...
El modelo no funcionó muy bien para lo que se lo
había pensado inicialmente, pero mucho despuésse descubrió que servía perfectamente para calcular
el número de ancestros de una abeja macho: el zángano nace de
un huevo sin fecundar; tiene, por tanto una madre y ningún padre. Su madre, en
cambio, sí tuvo dos padres, de tal manera que el original tiene dos abuelos y
tres bisabuelos, dos de su abuela y uno de su abuelo, y así sucesivamente,
completando la serie de Fibonacci.
Aquí les dejo un video que me ha parecido bastante interesante y que refleja claramente lo comentado anteriormente.
Bibliografia:
- http://www.elblogalternativo.com/2009/04/22/las-matematicas-se-pueden-ver-en-la-naturaleza-libro-anda-con-ojo-de-pilar-moreno/
-http://es.noticias.yahoo.com/blogs/cuaderno-de-ciencias/las-matem%C3%A1ticas-ocultas-en-la-naturaleza-121208815.html
http://catedu.es/matematicas_mundo/NATURALEZA/Naturaleza.htm
Tarea 6 Publicar una ecuación
La tarea 6, lo que quiere es que tengáis herramientas que os permitan expresar ideas matemáticas mediante cualquier medio.
Para ello necesitáis poder meter ecuaciones, en cualquier texto matemático que escribáis.
Se necesita disponer de un editor de ecuaciones, uno de los más cómodos que hay en la red es: http://rinconmatematico.com/latexrender/
En el podemos generar cualquier ecuación, esto nos dará una imagen que podremos copiar en nuestro POST.
LO QUE HAY QUE HACER
a) Haz una entrada en el Blog de clase con una ecuación matemática que incluya alguna integral y alguna una fracción.
a.1) Primero tendrás que generar la ecuación que quieras con el editor de ecuaciones http://rinconmatematico.com/latexrender/
a.2) Hacer un post con esa ecuación
b) Tendrás que rellenar el formulario de la tarea 6, con la dirección de la entrada que has realizado
Valoración: 2 horas de trabajo.
Plazo: Antes de que finalice Octubre, pero recomendamos que tomes tiempo, para resolver los problemas que vayan surgiendo
Ejemplo de entrada con una ecuación http://ademat.blogspot.com.es/2012/10/ejemplo-de-ecuacion.html
Tarea Nº 5 Hoja de Ejercicios de Derivadas de 1 variable
En este enlace esta la pagina de ejercicios
https://docs.google.com/document/d/1A8Ls83fega2o02xAU-KzbHqC_tINMKtuPE-UnVPrCmU/edit
Debéis de hacerla en papel. Poner en la parte de arriba, a la derecha, nombre del alumno y dirección de correo GOUMH
Valoración 2 horas de trabajo
Tenéis que rellenar también el formulario Nº 5, (en el tenéis que escribir lo que dan las derivadas, pero con las limitaciones que da el tener que escribirlo como texto)
Plazo de entrega: Hasta el Miércoles 10 de Octubre a las 8:30
miércoles, 3 de octubre de 2012
Phi en la sucesión de Fibonacci
Phi en la sucesión de Fibonacci
Este numero se puede hallar también con la sucesión de Fibonacci. Esta sucesión matemática es la siguiente:
1-1-2-3-5-8-13-21-34-55-89-144-233...
Esta numeración consiste en sumar el anterior número para descubrir el siguiente, por ejemplo el siguiente a 8 es 8+5=13.
¿Pero que tiene que ver esta sucesión con el número áureo?
Pues vea la siguiente tabla:
Cociente entre un numero de la sucesión y su inmediatamente anterior
|
Diferencia entre el cociente expuesto a la izquierda y el número áureo
|
1 ÷ 1 = 1
|
- 0,618034
|
2 ÷ 1 = 2
|
+ 0,381966
|
3 ÷ 2 = 1,5
|
- 0,118034
|
5 ÷ 3 = 1.666667
|
+ 0,048633
|
8 ÷ 5 = 1,6
|
- 0,018034
|
13 ÷ 8 = 1,625
|
+ 0,006966
|
21 ÷ 13 = 1,615385
|
- 0,002649
|
34 ÷ 21 = 1,619048
|
+ 0,001014
|
55 ÷ 34 = 1,617647
|
- 0,000387
|
89 ÷ 55 = 1,618182
|
+ 0,000148
|
144 ÷ 89 = 1,617978
|
- 0,000056
|
233 ÷ 144 = 1,618056
|
+ 0,000022
|
Comprobamos que paso tras paso nos acercamos más al número Phi. Las diferencias son cíclicas, cada vez más cerca de Phi y una vez la aproximación es por debajo del valor de phi, la vez siguiente por encima y así hasta el infinito... Es un logaritmo.
Phi en el triángulo de Pascal
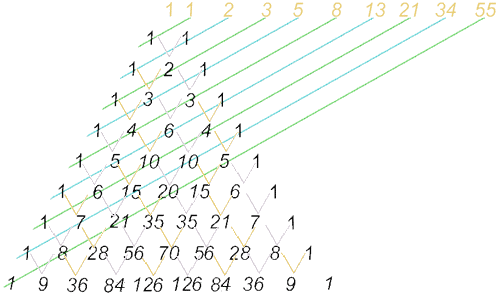
Este es el triángulo de Pascal que se forma situando el número uno por sus dos laterales y los demás números se hallan sumando los dos números que tiene justo encima (según las V del dibujo). Sumando los números según las diagonales (líneas verdes y azules en el dibujo) obtenemos la sucesión de Fibonacci.
Si cogemos la tercera linea diagonal: 1-3-6-10-15-21-28-36... Y sumamos una numero a la siguiente obtenemos los cuadrados sucesivamente de cada numero:
• 1 + 3 = 4 que es el cuadrado de 2 (2² -> 2x2=4)
• 3 + 6 = 9 que es el cuadrado de 3 (3² -> 3x3=9)
• 6 + 10 = 16 que es el cuadrado de 4 (4² -> 4x4=16)
Así prodriamos seguir hasta el infinito.
línea áurea
La razón entre el segmento entero y el segmento a es la misma que la razón entre los segmentos a y b, esta es la razón áurea.
(a+b)/a = a/b -> a² = b(a+b) = ba+b² -> a² - ba - b² = 0
Para averiguar el valor de a vamos a solucionar esta última ecuación de segundo grado.
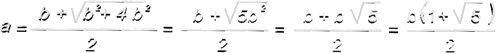
a/b = Φ ->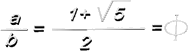 
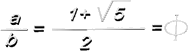
Como ha visto el arte tiene mucho que ver con las matemáticas y estas a su vez intentan dar explicaciones lógicas a la naturaleza y este universo tan grande y curioso.
Por lo tanto es lógico que el hombre utilice las matemáticas para representar a través del arte este universo que nos rodea.
También es lógico que empleemos herramientas basadas en las matemáticas para crear arte.
BIBLIOGRAFIA:
martes, 2 de octubre de 2012
Las matemáticas y la naturaleza
Las Teselaciones de Voronoi, también conocidas como Polígonos de Thiessen
son formaciones geométricas que se basan en un patrón de distribución que
resulta fácilmente reconocible en muchas estructuras naturales, como las alas
de los insectos o las ramificaciones capilares vegetales.Veamos un sistema muy intuitivo de entender cómo se conforma una Teselación de Voronoi:
Imaginad que tenemos dos puntos: uno rojo y otro azul (arriba
a la izquierda). Empezamos trazando una línea que los une y después otra
perpendicular que se halle justo en la mitad. Acabamos de hallar la mediatriz del segmento de unión de estos dos puntos.
Arriba a la derecha añadimos un tercer punto verde y generamos dos nuevas mediatrices, que se interseccionan con la primera.
Si seguimos añadiendo puntos podremos ir generando sucesivas mediatrices que, con sus intersecciones, darán lugar a una serie de polígonos —Teselas de Voronoi— alrededor de un conjunto de “puntos de control”. De esta manera, el perímetro de los polígonos generados es equidistante a los puntos vecinos y designa su área de influencia.
Los segmentos que unen directamente los puntos forman una estructura triangular conocida como Triangulación de Delaunay.
Arriba a la derecha añadimos un tercer punto verde y generamos dos nuevas mediatrices, que se interseccionan con la primera.
Si seguimos añadiendo puntos podremos ir generando sucesivas mediatrices que, con sus intersecciones, darán lugar a una serie de polígonos —Teselas de Voronoi— alrededor de un conjunto de “puntos de control”. De esta manera, el perímetro de los polígonos generados es equidistante a los puntos vecinos y designa su área de influencia.
Los segmentos que unen directamente los puntos forman una estructura triangular conocida como Triangulación de Delaunay.
En realidad, si tenemos una serie de puntos aleatorios
dispersos en el plano, la mejor forma de hallar la Telesación de
Voronoi correspondiente a ese conjunto es partir de la Triangulación
de Delaunay. Y de hecho ese es precisamente el orden que se muestra en las imágenes: primero aparece la Triangulación de Delaunay y posteriormente la Teselación de Voronoi.
Pero para poder trazar una correcta Triangulación de Delaunay es necesario que se cumpla la conocida como “Condición de Delaunay”: una red de triángulos es una triangulación de Delaunay si todas las circunferencias circunscritas de todos los triángulos de la red son “vacías”.
Fijaos que realmente, dados un número determinado de puntos en el plano no existe una única manera de unirlos formando triángulos, existen muchísimas. Pero sólo una posible triangulación cumple con la mencionada condición. Es muy simple: trazaremos un triángulo usando 3 puntos sólo si se cumple que la circunferencia circunscrita a esos 3 puntos es “vacía” (no encierra ningún otro punto). Podéis verlo en la siguiente gráfica:
Pero para poder trazar una correcta Triangulación de Delaunay es necesario que se cumpla la conocida como “Condición de Delaunay”: una red de triángulos es una triangulación de Delaunay si todas las circunferencias circunscritas de todos los triángulos de la red son “vacías”.
Fijaos que realmente, dados un número determinado de puntos en el plano no existe una única manera de unirlos formando triángulos, existen muchísimas. Pero sólo una posible triangulación cumple con la mencionada condición. Es muy simple: trazaremos un triángulo usando 3 puntos sólo si se cumple que la circunferencia circunscrita a esos 3 puntos es “vacía” (no encierra ningún otro punto). Podéis verlo en la siguiente gráfica:
Una vez que tenemos definida la Triangulación
de Delaunay (arriba a la izquierda) podemos ir girando 90º cada uno de los segmentos de los triángulos por el punto medio para dar con la Teselación de Voronoi. Exactamente lo que muestra la imagen justo antes de alejarnos y mostrar la estructura del ala de nuestra libélula.
FUNCIÓN LOGÍSTICA
La función logística, curva logística o curva en forma de S es una función matemática que aparece en diversos modelos de crecimiento de poblaciones, propagación de enfermedades epidémicas y difusión en redes sociales. Dicha función constituye un refinamiento del modelo exponencial para el crecimiento de una magnitud. Modela la función sigmoidea de crecimiento de un conjuntoP.
El estudio inicial de crecimiento es aproximadamente exponencial; al cabo de un tiempo, aparece la competencia entre algunos miembros de P por algún recurso crítico K ("cuello de botella") y la tasa de crecimiento disminuye; finalmente, en la madurez, el crecimiento se detiene.
La función logística simple se define mediante la fórmula
donde la variable P puede ser considerada o denotada como población, donde e es la constante de Euler y la variable t puede ser considerada el tiempo.1 Para valores de t en el rango de los números reales desde −∞ a +∞, la curva S se puede obtener. En la práctica, dada la naturaleza de la función exponencial, e−t, es suficiente con computar t para un pequeño rango de números reales como pueden ser [−6, +6].
En su forma más general, la función logística se define por la fórmula matemática:
. Estas funciones tienen un campo de aplicación muy amplio, desde la 
Matemáticas & Entretenimiento:Teorema de Flood Fill
www.microsiervos.com
www.microsiervos.com
Si quieres comprobar si el teorema de los cuatro colores es cierto, nada más fácil que jugar un rato a Flood Fill [Flash], un sencillo juego que está basado precisamente en esta idea. El juego comienza con unas pocas regiones que hay que colorear con el ratón y se va complicando poco a poco, pero siempre hay únicamente hay cuatro colores disponibles. Pese a que a veces parece casi imposible todos los mapas tienen solución. (Detalle importante: dos regiones que se toquen en un solo punto no se consideran conectadas).
Y es que aunque se intuía que el teorema era correcto en 1976 Kenneth Appel y Wolfgang Haken publicaron la demostración definitiva, con ayuda de un ordenador que examinó millones de mapas. El teorema era cierto y cuatro colores bastaban para colorear cualquier mapa según el planteamiento original.
Curiosamente, da igual que el mapa esté limitado a un cuadrado como en este juego o sobre una superficie cilíndrica (como la del Pac-Man, en la que se «tocan» dos laterales) o incluso que esté sobre la superficie de una esfera como un globo terráqueo. Tan solo cuando el mapa está dibujado enrevesadamente sobre una superficie toriodal la cosa se complica y son necesarios hasta 7 colores.
Constante aparcamiento Rényi
LA CONSTANTE DE APARCAMIENTO DE RÉNYI
La constante de aparcamiento de rényi trata de estimar el espacio que se utiliza realmente para aparcar en una línea recta. La cifra a la que llega, es que se utiliza aproximada mente un 74,76% del espacio, que equivale a la densidad media:unos 0,75 coches por coche teórico o espacio de coche.
Es decir,en 100 metros de acera, tan solo 74,76 metros estarían ocupados por coches, el resto sería espacio libre.
Es decir,en 100 metros de acera, tan solo 74,76 metros estarían ocupados por coches, el resto sería espacio libre.
BIBLIOGRAFIA:
WWW.MICROSIERVOS.COM
:
lunes, 1 de octubre de 2012
Las matemáticas ocultas en la naturaleza
 |
| Espirales en un cactus. (Marozols/Wiki Commons) |
Los más habituales son dos: el número áureo (o proporción áurea) y la serie de Fibonacci, que además están muy relacionados entre sí. En ambos casos, su desarrollo puede ser complicado de entender, pero podemos descubrirlos de manera natural. Para que lo entiendas, nadie calcula si la distancia entre la nariz y la barbilla es proporcional a la longitud total de la cara, pero si es así, consideramos a esa persona bella.
El número áureo es igual a 1,618... Las espirales áureas se alejan del centro con esta proporción cada cuarto de vuelta; de este modo, también se disponen las hojas en las ramas, o las ramas en los troncos. No se trata de una coincidencia, sino que es la manera más efectiva de organizar las estructuras. Ese patrón permite, entre otras cosas, que las ramas crezcan sin hacerse sombra las unas a las otras.
 |
| Alcachofa. (Wiki Commons) |
domingo, 30 de septiembre de 2012
¿ saben las abejas matemáticas?
Al almacenar la miel, las abejas deben que resolver un serio problema: necesitan guardarla en celdillas individuales, de tal manera que formen un mosaico sin huecos ni salientes entre las celdillas, con objeto de aprovechar el espacio al máximo.
De entre todas las posibles figuras geométricas las abejas escogieron el hexágono, pero está elección no fue arbitraria, sino que se fundamenta en lo que podría denominarse una lógica matemática.
El matemático Papus había demostrado que, entre todos los polígonos regulares con el mismo perímetro, encierran mas área aquellos que tengan mayor número de lados. De hecho, la figura que encierra mayor área para un perímetro determinado es el círculo, con un número infinito de lados.
No obstante, un círculo deja espacios cuando se rodea de otros círculos. Así, de todas las figuras geométricas que cumplen la condición “mayor número de lados y adyacencia sin huecos”, para la matemática es el hexágono la más óptima. Aunque para las abejas esto es verdad desde su nacimiento.
Un hexágono tiene 9 diagonales, resultado que se puede obtener aplicando la ecuación general para deteminar el número de diagonales de unos polígonos,
; siendo el número de lados 
, tenemos:
La suma de todos los ángulos internos de cualquier hexágono es 720 grados ó
radianes.
deducción: no podemos asegurar que las abejas sean capaces de realizar esos cálculos para hacer sus colmenas , pero si podemos decir que la naturaleza es sabia y que gracias a su forma de trabajar sabemos que entre todos los polígonos regulares encierran má áreas los que tienen mayor número de lados
De entre todas las posibles figuras geométricas las abejas escogieron el hexágono, pero está elección no fue arbitraria, sino que se fundamenta en lo que podría denominarse una lógica matemática.
El matemático Papus había demostrado que, entre todos los polígonos regulares con el mismo perímetro, encierran mas área aquellos que tengan mayor número de lados. De hecho, la figura que encierra mayor área para un perímetro determinado es el círculo, con un número infinito de lados.
No obstante, un círculo deja espacios cuando se rodea de otros círculos. Así, de todas las figuras geométricas que cumplen la condición “mayor número de lados y adyacencia sin huecos”, para la matemática es el hexágono la más óptima. Aunque para las abejas esto es verdad desde su nacimiento.
Un hexágono tiene 9 diagonales, resultado que se puede obtener aplicando la ecuación general para deteminar el número de diagonales de unos polígonos,
; siendo el número de lados , tenemos:La suma de todos los ángulos internos de cualquier hexágono es 720 grados ó
radianes.deducción: no podemos asegurar que las abejas sean capaces de realizar esos cálculos para hacer sus colmenas , pero si podemos decir que la naturaleza es sabia y que gracias a su forma de trabajar sabemos que entre todos los polígonos regulares encierran má áreas los que tienen mayor número de lados
Suscribirse a:
Entradas (Atom)