Irene Sansano Santonja - Tarea 7C

Irene Sansano Santonja - Tarea 7B

Irene Sansano Santonja - Tarea 7A

Ley de los grandes números

Al realizar reiteradamente una experiencia aleatoria, la frecuencia relativa de un cierto suceso, fr(S), va tomando distintos valores. Estos valores al principio sufren grandes oscilaciones pero, poco a poco, se van estabilizando (oscilan cada vez menos). Cuando N crece mucho, se aproximan a un cierto valor que es la probabilidad de S, P[S].

LEY DE LOS GRANDES NÚMEROS

Por ejemplo, al lanzar un dado se obtienen los valores de fr(3) para N = 20, 40, 60, 80, 100, 120, ...
Los valores de fr(3) se van estabilizando en torno a 1/6=0,166.

Podemos comprobar el ejemplo dado en el simulador siguiente: Ley de los grandes números.
Solo tenemos que marcar el tres antes de lanzar "muchas veces".

"Pantallazo" del simulador para fr(3), Autor aplicación: Manuel Sada

¿Por qué la frecuencia relativa tiende a estabilizarse?

Al lanzar reiteradamente un dado, ¿es posible obtener el suceso "3" cinco veces consecutivas? Por supuesto que sí; es difícil, pero posible. ¿Cómo afecta esa racha a la fr(3)? Pues depende de cuántas experiencias se lleven. Por ejemplo, supongamos que antes de la racha era fr(3)=0,16:

Con la racha de 5 veces "3", fr(3) aumenta 4 centésimas.

fr(3) aumenta 4 milésimas.

fr(3) aumenta 4 diezmilésimas.

Es decir, fr(3) se estabiliza porque, al ser el denominador cada vez más grande, al cociente le afectan cada vez menos las fluctuaciones del numerador.

David Marín García - Tarea 7C

David Marín García - Tarea 7B

Aqui dejo mi publicación en ISSUU

Santiago Belda Palazón - Tarea A

Método de integración por partes



Enlace a la ecuación

M ÁNGELES LÓPEZ TAREA 7 C VIDEO POWTOON

Aquí os dejo un pequeño vídeo sobre algunos Tips Para Prepara Selectividad, Espero que os guste:

David Marín García - Tarea 7A

A continuación tenemos la matriz de Vandermonde de orden n.

Se puede demostrar que el determinante de esta matriz es el siguiente:

Prueba

Prueba blog EPSO David Marín.

Beatriz Méndez Mira - Tarea 7C

¡Hola! Aquí tenéis un vídeo explicativo que os ayudará a plantear y resolver problemas con ecuaciones de  1er grado y una incógnita. También lo podéis ver pinchando AQUÍ.

Javier Ludeña Nicolás. TAREA B

Aquí os dejo mi publicación en ISSUU:

M ÁNGELES LÓPEZ TAREA 7 B PUBLICACIÓN ISSUU

Os dejo la presentación publicada en ISSUU,



También os dejo el enlace, para ello ckick aquí

M ÁNGELES LÓPEZ TAREA 7 A - ECUACIONES

Me gustaría mostraros a partir de una captura (imagen) un ejemplo de ecuación a través del editor de Ecuaciones Atomur, este es  tan sólo un ejemplo, pero la aplicación tiene infinidad de posibilidades:

Otro ejemplo La transformada de Fourier, imprescindible para la comprensión de las estructuras de ondas más complejas:

M ÁNGELES LÓPEZ PRUEBA

Prueba de la Tarea 7

Rafael Fernández González - Tarea 7B

A continuación dejo el enlace de un documento subido ISSUU.

Enlace ISSUU

Rubén Tormo Llorens: Tarea 7C

A continuación podéis ver el Powtoon que he creado para la Tarea 7C:
También os dejo un enlace directo al vídeo:

Javier Ludeña Nicolás - TAREA A

Vamos a resolver la siguiente integral:

En primer lugar, factorizamos el denominador y hacemos la suma:

Como las dos fracciones tienen el mismo denominador, los numeradores han de ser iguales:

Calculamos los coeficientes de A, B y C dando a la x los valores que anulan el denominador:

Finalmente, se calculan las integrales de las fracciones simples:

Rafael Maciá Fernández - Tarea 7B

Rafael Maciá Fernández - Tarea 7A

Resolución de sistemas de ecuaciones lineales de dos incógnitas

El siguiente sistema será el que resolvamos por los tres métodos ya explicados:

Método de reducción

a) Obtenemos un sistema equivalente. Elegimos una incógnita en las dos ecuaciones, en este caso y. Multiplicamos la segunda ecuación por 5. 

Nuestro sistema equivalente es:

 

b) Restamos las dos ecuaciones del sistema para eliminar la y.

 

c) Resolvemos la ecuación de una incógnita que resulta.

d) Sustituimos el valor obtenido en una de las dos ecuaciones del sistema, en este caso
en la segunda ecuación.

 

e) Comprobamos el resultado

Por tanto la solución x=2, y=1 es correcta.

Método de sustitución

a) Elegimos para despejar la incógnita y de la segunda ecuación.

b) Sustituimos esta incógnita en la primera ecuación.

  

c) Resolvemos la ecuación de una incógnita que resulta.

d) Sustituimos el valor obtenido en una de las dos ecuaciones del sistema, en este caso
en la segunda ecuación.

 

e) Comprobamos el resultado

Por tanto la solución x=2, y=1 es correcta.

Método de igualación

a) Elegimos para despejar la incógnita y de las dos ecuaciones.

b) Igualamos las expresiones obtenidas.

c) Resolvemos la ecuación de una incógnita que resulta.

d) Sustituimos el valor obtenido en una de las dos ecuaciones del sistema, en este caso
en la segunda ecuación.

 

e) Comprobamos el resultado

Por tanto la solución x=2, y=1 es correcta.

prueba

1,2,3

TAREA 7C) NADIA MARÍA GUERRERO MARTÍNEZ

TAREA 7C) NADIA MARÍA GUERRERO MARTÍNEZ 

Aquí os presento un vídeo para recordar a los alumnos que deben repasar las ecuaciones de primer grado antes de comenzar las sesiones de ecuaciones (3º de ESO).

TAREA 7B) NADIA MARÍA GUERRERO MARTÍNEZ

TAREA 7B) NADIA MARÍA GUERRERO MARTÍNEZ

Aquí os presento el Dossier de Problemas que he ido trabajando con los alumnos de 3º de ESO del IES Azud de Alfeitamí durante mis prácticas. En la última página incluí dos catálogos de ofertas en las que aparecen porcentajes para que apliquen lo aprendido a problemas cotidianos.

Beatriz Méndez Mira - Tarea 7B

A continuación, se propone un cuestionario tipo test para repasar los conceptos teóricos e introducción a los problemas en la unidad de Sistemas de ecuaciones para el curso 3º ESO. También puedes acceder al archivo a través de este ENLACE.

 

Vanessa Francés - Tarea 7C

¡Hola! Aquí tenéis un pequeño vídeo explicativo sobre FUNCIONES LINEALES. También os dejo el enlace directo al vídeo. 

Ana del Río Lozano - Tarea 7B

A continuación puedes consultar una propuesta didáctica para trabajar el Teorema de Thales:
 

Patricia Marco López - Tarea 7C

Aquí os dejo el vídeo que he hecho sobre cómo resolver un sistema de ecuaciones por el método de sustitución.

¡Espero que os guste!

 

Patricia Marco López - Tarea 7B

Aquí os dejo una serie de ejercicios resueltos del tema de sistemas de ecuaciones para el curso de 2º de la ESO:



Si queréis ver el documento en la página de Issuu, podéis hacerlo pinchando en el siguiente enlace: Sistemas de Ecuaciones de 2º ESO

Tarea 7B Antonio Pérez Muñoz

El documento que he escogido compartir es el libro"Detectives" del divulgador argentino Adrián Paenza. Es un libro sobre matemática recreativa que me ha parecido muy divertido.

Aquí os dejo el enlace al documento:
https://issuu.com/antonioperezmunoz/docs/detectives

Tarea 7A Antonio Pérez Muñoz

Se ha utilizado el TeX equation editor para realizar la resolución del siguiente límite:
Con este editor podemos llegar hasta el infinito y mas allá!! ;)

Arturo Sánchez Martínez. Tarea 7C.

Vídeo con Powtoon sobre operaciones matemáticas que, en principio, no tienen solución: Operaciones Imperdonables

TAREA 7A) NADIA MARÍA GUERRERO MARTÍNEZ

TAREA 7A) NADIA MARÍA GUERRERO MARTÍNEZ

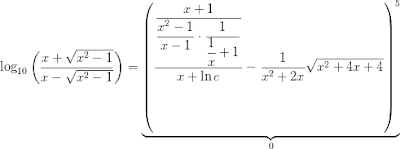
Aquí os presento una de esas ecuaciones que “asusta” a nuestros alumnos, pero que con un poco de destreza a la hora de realizar cálculos algebraicos se convierte en uno de los tipos más sencillos de ecuaciones logarítmicas. Esta facilidad se debe a que, como ya se anticipa en la ecuación que os presento, en la parte derecha se obtiene el valor 0.

Prueba Nadia María Guerrero Martínez

Esta entrada es prueba de que puedo publicar.

Rubén Tormo Llorens: Tarea 7B

Demostración de que 1+1=2 en realidad se puede convertir en una elegante, legible, sucinta y comprensible ecuación:


Además pulsando en la imagen tenéis acceso directo al enlace del documento:

Sara Guirado - Tarea C

Aquí tenéis mi vídeo, espero que os guste 😃

Patricia Marco López - Tarea 7A

A continuación os dejo un ejemplo de resolución de una integral por el método de cambio de variable.

La integral a resolver es:

Para su resolución hay que realizar el siguiente cambio de variable:

Una vez hecho el cambio de variable y resolviendo, queda:

Una vez resuelta la integral hay que deshacer el cambio de variable que se ha hecho antes:

Sara Guirado - Tarea B

He subido a Issuu juegos didácticos relacionados con las matemáticas.

Pedro Luis Díaz Sánchez - Tarea 7C

He creado este video en Powtoon para aplicar conceptos de porcentajes y reglas de tres:

Aquí podéis ver una previsualización:



Y aquí un enlace directo para verlo en Powtoon:
https://www.powtoon.com/c/blRXUry6EOg/1/m

Pedro Luis Díaz Sánchez - Tarea 7B

He subido a Issuu el libro de Matemáticas de 1º de ESO de Marea Verde.

Aquí una previsualización:

Y aquí en enlace directo al documento:

https://issuu.com/pedroluisdiazsanchez/docs/murcia_1eso

Pedro Luis Díaz Sánchez - Tarea 7A

Función de distribución normal, como resultado de la integración de la función de densidad.

El código que he utilizado es el siguiente:

F (x) = P [X \leq x] =  \frac{1}{ \sigma  \sqrt{2 \pi} }  \int_  {-\infty} ^x  e^{- \frac{(t- \mu )^2}{2 \sigma^{2} } }  dt

Marta Aguirrezabala. Tarea 7B

Muestra de diferentes ejercicios resueltos de fórmulas trigonométricas

María López García - Tarea 7 B

En esta entrada os dejo un pdf propio sobre el Método de Cramer para la resolución de sistemas:

Marta Aguirrezabala. Tarea 7A

Sabiendo que: 

Halla :

María López García - Tarea 7 A

Si tenemos el siguiente sistema:

Donde las incógnitas son:

Tenemos un sistema lineal cuya matriz de coeficientes es:

Esta matriz recibe el nombre de Matriz de Vandermonde y su determinante viene dado por el producto de todas las diferencias entre las abcisas de los puntos: