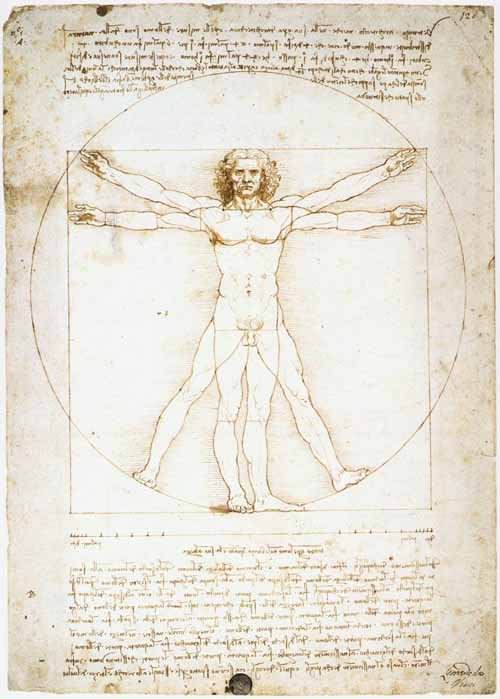
Leda Atómica

Leda atómica está pensada siguiendo la divina proporción según Luca Paccioli, del Renacimiento italiano. Leda y el cisne se inscriben en un pentágono en el interior del cual se ha insertado una estrella de cinco puntas de la cual Dalí realizó diversos estudios. La armonía de las referencias ha sido calculada por el artista según el matemático Matila Ghyka que entonces enseñaba en la Universidad de San Diego. Sus trabajos demuestran que la divina proporción es el fundamento de toda obra. Dalí, en contra de lo que piensan sus contemporáneos, que las matemáticas distraen / interrumpen la inspiración artística considera que cualquier obra de arte para serlo debe fundamentarse en la composición, en el cálculo.

Por ahora digamos que se trata de la división de una dada longitud en dos segmentos de forma tal que la longitud total (a+b) es al segmento mayor (a) como este es al segmento menor (b). O sea (a+b)/a = a/b.

Si llamamos φ = a/b, la ecuación anterior puede escribirse como 1 + 1/φ = φ, cuya solución positiva es

Este es el "número áureo". Matemáticamente se trata de un número irracional (pues no puede escribirse como una fracción, es decir como un cociente de dos números enteros) y algebraico (pues es solución de una ecuación polinómica, en este caso de segundo grado).

En el caso particular del pentagrama usado por Dalí en Leda atómica, y según se muestra en la siguiente figura, el segmento rojo es al segmento verde, como este es al azul y como este a su vez es al púrpura, y todos ellos en una relación dada por el número áureo.

Bibliografía: http://ciencia-arte.blogspot.com.es/2011/06/leda-atomica-y-aurea.html

LAS MATEMÁTICAS EN LA VIDA REAL.

La ciencia de las matemáticas constituye una de las herramientas más importantes para la vida cotidiana, pese al desconocimiento que existe sobre ella. La mayoría de las cosas se organizan a partir de los números, pero las matemáticas están presentes en más aspectos de lo que se suele pensar, desde la navegación en mar abierto hasta la telefonía móvil o el vuelo de los aviones.

Las matemáticas trabajan con un sistema numérico creado hace más de 1.500 años (unos 450 si hablamos de los decimales) y que hoy es clave, por ejemplo, para los biólogos empeñados en descifrar la información de la molécula de ADN descubierta en 1956 por James Watson y Francis Crick.

Arquitectura: puentes colgantes

El cálculo infinitesimal tiene múltiples repercusiones en la vida humana, aunque posiblemente la más destacada de ellas haya sido el descubrimiento de la curva necesaria para que un puente colgante no se desplome, conocida como catenaria. Esta aplicación fue descrita en el año 1691 por Johann Bernoulli, basándose en la mecánica y las leyes de movimiento de Isaac Newton. Bernoulli descartó la hipótesis de que la figura correcta era una parábola –aunque es cierto que los cables de suspensión de los puentes son parabólicos, lo que ocurre porque, además de su peso, soportan el del puente–.  Igualmente, este cálculo es básico para trazar la trayectoria de las sondas espaciales, calcular el desplazamiento de vehículos, o incluso estudiar la difusión de epidemias. De hecho muchas de las intervenciones que se ponen en marcha contra estos problemas de salud pública se basan en el cálculo infinitesimal.

                                   IMAGEN DEL GOLDEN GATE, EN SAN FRANCISCO (EEUU)

Comunicación: telefonía móvil

El teléfono móvil hace un uso esencial de la geometría de espacios multidimensionales, igual que la conexión a Internet, la televisión por satélite o cable y prácticamente cualquier otro aparato tecnológico que envíe o reciba mensajes. La comunicación moderna, en cualquiera de sus modalidades, es digital, con lo que todos los mensajes, incluidos los de voz, se convierten en pautas binarias basadas en los números 0 y 1. Pero las comunicaciones no son útiles si no son fiables: existe la posibilidad de que el mensaje recibido tenga alteraciones respecto al enviado, y el hardware electrónico no puede garantizar la precisión porque las interferencias e incluso un rayo cósmico pueden producir errores. Por ello, los ingenieros usan técnicas matemáticas basadas en los espacios multidimensionales para codificar las señales, de forma que el sistema puede detectar y corregir las imprecisiones.

Bibliografia:http://www.publico.es

LA GEOMETRÍA DEL HUEVO

Un huevo de ave es algo cotidiano en la vida de las personas, los podemos comer cocidos o fritos, con tomate o con patatas, pero ¿por qué tienen los huevos esa forma? Indudablemente parece que la historia evolutiva podría responder a esta pregunta al ser la forma del huevo la más provechosa para el éxito reproductor. Pero ¿responde esta forma ovalada a alguna norma matemática esta forma? ¿Podrían estos conocimientos acerca del huevo tener alguna aplicación para el hombre? La respuesta a ambas sería SÍ.

Triple arco característico de la arquitectura libanesa.

Definida por F, la geometría del huevo de gallina en su forma paradigmática tiene en su segmento característico una parábola. Aunque conocer qué ocurre en el proceso de producción del huevo no es significativo para el conocimiento de la parábola o para el diseño de los arcos parabólico y apuntado, admira que solamente en la última parte de ese muy rápido proceso el huevo adquiera la proporción configurada por F, como origen de resistencia y belleza, para recién consolidarse en contacto con la atmósfera.

El dibujo con arcos de cuatro círculos es el que mejor configura a la sección oval inscrita en la vesica piscis. Aunque en ese dibujo no se encuentra una parábola, se tiene de ésta con precisión las proporciones de su cuerda y flecha. La minúscula diferencia entre la parábola y la combinación de arcos circulares en partes no significativas (ver el gráfico de la parábola), hace que el producto del análisis de la figura oval sirva para el rápido diseño de los arcos parabólico y apuntado y para un mayor conocimiento de la parábola.

Con el conocimiento o percepción de la armonía en las proporciones e inspirada en la forma del huevo, la arquitectura que prefirió los arcos apuntado y parabólico utilizó adobes y mortero de barro en muy antiguas culturas de diferentes lugares, hasta llegar a la música en piedra de la arquitectura gótica, para construir obras bellas y además durables. La preferencia por tales arcos se debió a que la regularidad armónica de éstos reúne óptimas condiciones estructurales para transmitir las cargas al suelo más directamente, con un mínimo de esfuerzos laterales.

Todas las parábolas son similares: aunque el tamaño varíe, las constantes de su configuración son las mismas para todas ellas. En consecuencia, al quedar demostrado que la parábola se encuentra en la sección oval configurada por F, se establece las proporciones relativas de las principales dimensiones de toda parábola: parámetro, flecha y cuerda, con las implicaciones consiguientes. Así mismo la coherencia armónica del conjunto que asocia la figura oval con la parábola permite confirmar la ubicación del foco de ésta.

 Bibliografía: http://webs.adam.es/

El póker y las matemáticas.

Aunque las matemáticas tienen un rol fundamental dentro del póker, la realidad es que no es necesario poseer muchos conocimientos sobre matemáticas pero se debe saber los conocimientos básicos para manejar nuestras posibilidades. 

Dentro del póker a estas posibilidades se les denominado odds y muestra la cantidad de sucesos favorables separados por “:” de los sucesos desfavorables (25% = 25:75 = 1:3).

Otro concepto matemático que se debe saber para jugar al póker es el de “Valor Esperado” (VE), que es la expresión de algo que esperamos que suceda por haber realizado una acción. 

Esto se debe a la estadística. La repetición de un suceso determinado, en determinadas circunstancias, nos dará una cifra que denominamos promedio. Esto es: en n repeticiones de un suceso, x veces tendremos un determinado resultado u ocurrencia.

En el póker, VE es la ganancia o perdida que se producirá por realizar dicha acción. Este VE no se da en una cifra exacta sino dentro de un contexto en concreto, por lo que VE no es infalible, VE infalible solo existe en el plano matemático. Dentro del póker lo único que hace es saber las probabilidades de tu mano, para saber si debes jugar o no. El póker es un juego de suerte y estrategia, pero las matemáticas son una herramienta de ayuda.

Bibliografía: http://poker-online.quepasada.com/las-matematicas-en-el-poker

La "divina" proporción en los girasoles.

A lo largo de la historia nos encontramos con muchos matemáticos que se esfuerzan por estudiar la relación entre el numero áureo o tambien denominado popularmente, " La divina proporción" con la naturaleza.

El número aureo se trata de un número algebraico irracional que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción entre segmentos de rectas.Una sección áurea es una división en dos de un segmento según proporciones dadas por el número áureo. La longitud total a+b es al segmento más largo a como a es al segmento más corto b.  

En la naturaleza las hojas  y los petalos de las plantas se distribuyen buscando siempre la mayor cantidad de luz posible. Por eso ninguna hoja crece verticalmente sobre la otra y siguen un orden. En el caso del girasol encontramos que la formación de sus flósculos sigue un determinado orden en el que suelen haber 55 espirales en un sentido y 89 en el otro, o bien 89 y 144. Esta formación sigue el orden de la sucesión de fibonacci en la que se encuentra el llamado número dorado o número aureo.

En conclusión, las matemáticas en general tienen gran relación con la naturaleza y ya no solo con el ejemplo de los girasoles que he nombrado aquí sino como por ejemplo también con el tamaño de las hormigas o las galaxias.

Aquí dejo un pequeño vídeo de los girasoles en su momento mas bello.

BIBLIOGRAFÍA: -Imagenes: http://www.soldeoaxaca.com.mx/a_017.php

http://www.fondospedia.com/fondo-girasoles-1254.php

-Información: -Wikipedia

La simetría al ∞

La simetría se define como la disposición de las diferentes partes de un sujeto de una forma ordenada y correspondiente. La simetría supone equilibrio, y según la Real Academia de la Lengua, la correspondencia exacta en forma, tamaño y posición de las partes de un todo.

No hay que tener miedo de las matemáticas, pues como muchos sabréis las matemáticas se encuentran en todos los elementos de nuestro alrededor desde la estructura de las casas, coches y demás productos creados por el hombre hasta la naturaleza que nos rodea . Además también nos dota de la capacidad de apreciar la presencia de las matemáticas en los mismos explicándonos el porqué de sus formas. Hay mucha gente que tiene dificultades para afrontar esta ciencia o que simplemente la encuentran aburrida pero intentaré que al menos en este post las matemáticas os resulten fáciles y que aprendáis cosas nuevas. En concreto os voy a hablar de la simetría:

Por si no lo habéis entendido bien os diré que algo es simétrico cuando al doblarlo por su eje de simetría las dos partes resultantes(planos) se corresponden. Para verlo aún mas claro os pediré que os fijéis en la forma de las alas de esta mariposa o este copo de nieve:

En ambas dos podemos observar el eje de simetría y cómo los focos coinciden por lo que solo queda decir que nos fijemos en que la simetría rodea nuestro entorno no solo en estos dos casos sino también en edificios la naturaleza los reflejos,etc y que los buenos conocedores de la matemática encuentran en ella placeres comparables a los que proporcionan la pintura, la música y la naturaleza. Admiran la delicada armonía de los números y de las formas y se maravillan cuando un nuevo descubrimiento abre una nueva perspectiva asi que intentemos este año disfrutar de las matemáticas.

     
Bibliografía:

_ Imágenes:
 - http://www.scienceinschool.org/print/518 + un pequeño retoque con el paint.
_ Información:
- http://www.um.es/aulasenior/saavedrafajardo/trabajos/simetria.pdf
- http://rodrigojil.cl/
- http://www.elalmanaque.com/acertijos/mates.htm

A LA DIVINA PROPORCION

A ti, maravillosa disciplina,

media, extrema razón de la hermosura

que claramente acata la clausura

viva en la malla de tu ley divina.

A tí, cárcel feliz de la retina,

áurea sección, celeste cuadratura,

misteriosa fontana de mesura

que el universo armónico origina.

A tí, mar de los sueños angulares,

flor de las cinco flores regulares,

dodecaedro azul, arco sonoro.

Luces por alas un compás ardiente.

Tu canto es una esfera transparente.

A tí, divina proporción de oro.

Rafael Alberti

Buenas, encontré estos bonitos versos del maestro Alberti y me parece que van que ni pintado.

Aquí os dejo un enlace de  un vídeo en el que el Pato DONALD muy gráficamente nos muestra una serie de animaciones matemáticas muy interesantes.

NO OS LO PERDÁIS.

http://www.youtube.com/watch?v=7h8dNH9Xnfg&playnext=1&list=PLCB5EE3231CEA028D&feature=results_video

Espiral de Durero

Alberto Durero (1471-1528) , fue el artista más famposo del Renacimiento alemán, y aporto grandes conocimientos al mundo de las matemáticas aplicadas en el arte. En 1525, tres años antes de su muerte, publicó un libro llamado ''Instrucción sobre la medida con regla y compás de figuras planas y sólidas''  En esta obra Durero muestra cómo trazar con regla y compás algunas espirales y entre ellas uno que pasará a la historia con su nombre, basada en la sección aurea y precedida por la sucesión de Fibonacci.

Diego de Silva Velázquez (1599-1660), pintor español, máximo representante de la pintura barroca en España. Creó la obras maestra "Las Meninas" (1656) Representa a la infanta Margarita, rodeada de dos meninas, de pie junto al pintor, quien mira hacia el espectador desde la parte izquierda del cuadro. Velázquez aparece pintando al rey Felipe IV y a la reina doña Mariana, cuya presencia sólo queda sugerida por el reflejo de sus efigies en el espejo situado al fondo de la habitación. 

En este caso de composición, la espiral nace en el centro del pecho de la Infanta Margarita de Austria. Las propiedades consolidadas de la espiral, y su crecimiento proporcional sobre la superficie de Las Meninas, es consecuencia de la disponibilidad natural de la Geometría y algo más que nos remite a un amplio significado: "Simbólicamente, este punto medio y anatómico del cuerpo de la Infanta Margarita de Austria, marca el centro reservado de los elegidos, en todos los casos, una imagen o identidad exclusiva de la verdadera semilla de los reyes del mundo, tal y como en la tradición europea el Emperador se situaba, siempre, en el lugar central  en las ceremonias". Esto se puede apreciar perfectamente en esta imagen ya desarrollada.

A lo largo de la historia, hay muchas obras de arte y arquitectura que han sido elaboradas siguiendo un patrón concreto, ya sea una sucesión a unas proporciones predeterminadas, y los más famosos pintores arquitectos y pintores se han regido por estas normas para elaborar muchas de sus grandes obras.




Vía: Simetría Espiral

El número áureo

Ésta fotografía representa el Partenón de Atenas, construido entre los años 447 y 432 a. C. y el cual está dedicado a la diosa de la sabiduría Atenea.

Como veremos, este templo es agradable a la vista ya que se basa en el rectángulo de oro; si dibujamos un cuadrado y marcamos el punto medio de uno de sus lados, Lo unimos con uno de los vértices del lado opuesto y llevamos esa distancia sobre el lado inicial, de esta manera obteniendo el lado mayor del rectángulo, y finalmente, obtenemos un rectángulo cuyos lados están en proporción áurea.

Por ello, el Partenón, es una importante obra arquitectónica, tanto por los materiales empleados en su construcción, como por la belleza que transmite debido a las proporciones aureas.

La Simetria en la naturaleza

        En este post, quiero hablar brevemente sobre un aspecto muy importante en nuestra vida común.

Se trata sobre la simetria.

Si pensamos un poco, podemos darnos cuenta que que las extrellas, las rocas, los planetas e incluso los seres vivos, tienen compuestos diferentes, es decir, que cada uno de ellos tiene una combinación de materia (gases, líquidos o solidos)..

Por lo que parte de esta materia contiene una propiedad bastante curiosa, como nosotros mismos ya podemos estar imaginándonos, y es que si la dividimos en dos, estas dos mitades son iguales, es decir, que son asimétricas, porque las vemos y se ven igual de un lado y desde el otro.

La imagen que muestro a continuación, es un ejemplo sencillo de la simetria de la naturaleza:

Con simbolos matemáticos, escribiríamos;

F(M/d) × (m/d)

      Los dos términos de la derecha de la ecuacíon, son "casi iguales" que los de la izquierda, es un ejemplo de la gravitación, expresando de que se puede establecer una simetria.

El resultado en la imagen sería igual, si la plegáramos, obtendriamos una unión total de las sombras que se reflejan en el agua; la torre, el puente, las farolas..

Fuentes:

- Foto propia

- http://es.wikipedia.org/wiki/Simetr%C3%ADa

GEOMETRÍA INNATA

 Las abejas, especie de insectos que poseen una organización social muy compleja, poseen la habilidad innata programada en sus genes de optimizar sus estructuras de almacenamiento de alimento mediante la geometría.

     Dicha optimización fue observada y constatada por el matemático griego Papus de Alejandrina (284 al 305) basándose en la forma hexagonal de que dotan las abejas a las celdillas para ahorrar espacio y esfuerzos al construirlas.

    De entre todas las figuras geométricas que podían haber "escogido" las abejas escogieron el hexágono  pero esta elección no la realizaron al azahar, sino que podría decirse que se fundamenta en una lógica matemática. 
     Esto significa que entre todos los polígonos regulares con el mismo perímetro, aquellos que poseen mayor área son los que tienen mayor numero de lados. La figura que encierra mayor área para un perímetro determinado es el circulo, con numero infinito de lados, no obstante, el circulo deja huecos cuando     se rodea de otros círculos.

     Así pues, Papus constato, que de todas las figuras geométricas que cumplen la condición de "mayor numero de lados y adyacencia sin huecos" para las matemáticas el hexágono es la mas optima.

 

las matematicas en el arte

Durante toda la historia del arte ha habido diferentes estilos y normas sobre las proporciones de las figuras talladas. Estas proporciones se basan en medidas matemáticas y geométricas tomando como modelo el cuerpo humano y con esto conseguir un procedimiento que ayude a crear.   También influyen consideraciones religiosas, estéticas, antropológicas y de "modas".

   Hay diferentes estudios sobre el cuerpo humano en los que se diferencia el hombre de la mujer. En la mujer la cabeza es mas larga en relación al cuerpo que en el hombre además sus formas están vinculadas a cilindros y globos por el contrario en el hombre con líneas y cubos.

   Los primeros criterios sobre proporción se originan en el antiguo Egipto. La escultura estaba directamente relacionada con las arquitectura, con esto las estatuas se tallan desde un cubo por pertenecer a sillares. Las proporciones eran medidas por un sistema cuadriculado en que la altura del hombre era de 18 a 24 cuadradillos según las épocas y 14 si estaba sentado. Con este método se determinaba la posición exacta de cada parte del cuerpo.

  Los griegos estudiaron extensivamente el cuerpo humano, durante la época helénica se crearon multitud de estatuas representando la figura humana. Policleto destacó por sus estudios, indicando que la belleza esta directamente relacionada con las proporciones numéricas del cuerpo humano. En su tratado "canon" determina relaciones matemáticas entre las diferentes partes del cuerpo.

   Vitruvio arquitecto-ingeniero autor del tratado de arquitectura "De Architectura" donde investigó la relación entre las artes y la matemáticas. Dentro del cuerpo humano estableció al ombligo ser el centro del cuerpo. Sabiendo que el hombre con los brazos extendidos tiene una anchura igual a su altura por lo que queda inscrito en un círculo y un cuadrado siendo el ombligo el centro del círculo. Se puede obtener el numero áureo de la relación que hay entre la distancia del ombligo a la punta de la mano y la altura del hombre.

Manuscrito del genial humanista Leonardo de Vinci.

El Quitasol

En este cuadro podemos ver una de las obras de Francisco Goya conocida como El Quitasol (1777) en el que utiliza una serie de elementos relacionados con las matemáticas.

En esta imagen podemos ver a simple vista a una muchacha sentada en un ribazo con un perrillo en el halda , y a su lado un muchacho en pie haciéndole sombra con un quitasol.

Podemos observar  en la imagen un triangulo y dos diagonales.

En cuanto a la composición, las líneas de fuerza dibujan casi un triángulo equilátero en el que se enmarca la muchacha. Por otro lado, todas las miradas convergen en el rostro de la joven, matizado por una sombra filtrada de suaves tonos verdes creados por el color de la sombrilla. El óvalo de la joven es una elipse regular y en ella se cruzan dos diagonales determinadas por la dirección de la mirada del mozo y la línea del muro de la izquierda, cuya perspectiva se ha forzado para que esta diagonal incida en el buscado centro de atención del cuadro.

FUNTES DE INFORMACION:

http://www.slideshare.net/Cristinamm/el-quitasol-presentation

http://es.wikipedia.org/wiki/El_quitasol

La ruleta puede no ser suerte

  Aunque se trate de un asunto muy debatido, muchos matemáticos afirman haber encontrado una forma de ganar a la ruleta en un casino.

  En los años 70, un joven universitario llamado Doyne Farmer, derrotó al casino jugando a la ruleta y no por mera suerte suya sino porque tenía los conocimientos necesarios y suficientes en matemáticas y computación para realizar cálculos que le otorgasen la victoria.

  En aquellos tiempos Farmer se negó a revelar sus secretos pero dos colegas suyos afirman que basta con un portátil y un teléfono para revertir las probabilidades de ganar en la ruleta a favor del jugador.

 Según Michael Small y Michael Tse, de universidades de Australia y Hon Kong, la clave para la victoria está en registrar el momento en que la pelota y la rueda giratoria pasan por un punto señalado de antemano. 

Los investigadores usaron un dispositivo de recuento parecido al de Farmer, acertando en qué mitad de la ruleta caería la pelota en 13 de 22 eventos; por otra parte, en 3 intentos el modelo predijo exactamente la casilla ganadora. Con esto, las probabilidades pasaron de 2.7% a favor de la casa, a 18% a favor del jugador (en ruletas de estilo europeo). Estas pruebas se realizaron otras 700 veces utilizando un sistema automatizado de grabación.

Farmer opinaba que los cálculos de sus amigos se diferenciaban de los suyos en que estos suponen que la principal fuerza que detiene el movimiento de la pelota es la fricción en la ruleta, aunque según él la verdadera responsable es la resistencia del aire.

http://www.roulettestar.com/probability

¿Te atreves con la ruleta? 

informacíon e imágen:

http://pijamasurf.com/2012/05/matematicos-revelan-metodo-para-ganar-en-la-ruleta-de-un-casino/

http://www.roulettestar.com/probability

Formulario Tarea 4 Ejercicios de sistemas

Tarea 4 Ejercicios de Sistemas de ecuaciones

Hay que resolver estos 3 Sistemas de ecuaciones por el Método del Gauss que es el que hemos visto de hacer pivotes, y ceros por debajo.

Plazo de entrega imporrogable: Lunes 1 de Octubre

Se entrega de dos formas (de las dos obligatoriamente) En papel el lunes, y antes del lunes rellenando el formulario para la tarea 4, donde solamente hay que poner los resultados

Valoración: 1 hora de trabajo. 

Presentación 3 Eliminación con Matrices (3)

Presentación 2 Algebra Lineal Idea de Eliminación (2)

Presentación 1 Álgebra lineal 1

Clase del 28 de Septiembre

Comenzamos la asignatura siguiendo 18.06 del MIT

http://ocw.mit.edu/courses/mathematics/18-06-linear-algebra-spring-2010/video-lectures/

Esta es una presentación de sistemas de ecuaciones lineales, que nos permite con facilidad visualizar los sistemas de ecuaciones lineales, con una representación por filas y una representación por columnas.