Phi en la sucesión de Fibonacci
Este numero se puede hallar también con la sucesión de Fibonacci. Esta sucesión matemática es la siguiente:
1-1-2-3-5-8-13-21-34-55-89-144-233...
Esta numeración consiste en sumar el anterior número para descubrir el siguiente, por ejemplo el siguiente a 8 es 8+5=13.
¿Pero que tiene que ver esta sucesión con el número áureo?
Pues vea la siguiente tabla:
Cociente entre un numero de la sucesión y su inmediatamente anterior
|
Diferencia entre el cociente expuesto a la izquierda y el número áureo
|
1 ÷ 1 = 1
|
- 0,618034
|
2 ÷ 1 = 2
|
+ 0,381966
|
3 ÷ 2 = 1,5
|
- 0,118034
|
5 ÷ 3 = 1.666667
|
+ 0,048633
|
8 ÷ 5 = 1,6
|
- 0,018034
|
13 ÷ 8 = 1,625
|
+ 0,006966
|
21 ÷ 13 = 1,615385
|
- 0,002649
|
34 ÷ 21 = 1,619048
|
+ 0,001014
|
55 ÷ 34 = 1,617647
|
- 0,000387
|
89 ÷ 55 = 1,618182
|
+ 0,000148
|
144 ÷ 89 = 1,617978
|
- 0,000056
|
233 ÷ 144 = 1,618056
|
+ 0,000022
|
Comprobamos que paso tras paso nos acercamos más al número Phi. Las diferencias son cíclicas, cada vez más cerca de Phi y una vez la aproximación es por debajo del valor de phi, la vez siguiente por encima y así hasta el infinito... Es un logaritmo.
Phi en el triángulo de Pascal
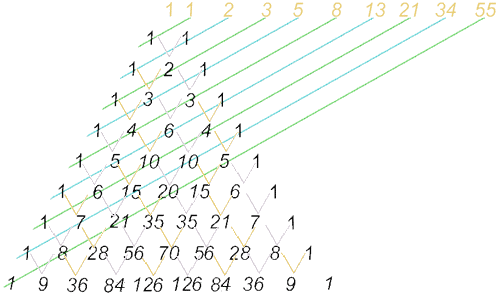
Este es el triángulo de Pascal que se forma situando el número uno por sus dos laterales y los demás números se hallan sumando los dos números que tiene justo encima (según las V del dibujo). Sumando los números según las diagonales (líneas verdes y azules en el dibujo) obtenemos la sucesión de Fibonacci.
Si cogemos la tercera linea diagonal: 1-3-6-10-15-21-28-36... Y sumamos una numero a la siguiente obtenemos los cuadrados sucesivamente de cada numero:
• 1 + 3 = 4 que es el cuadrado de 2 (2² -> 2x2=4)
• 3 + 6 = 9 que es el cuadrado de 3 (3² -> 3x3=9)
• 6 + 10 = 16 que es el cuadrado de 4 (4² -> 4x4=16)
Así prodriamos seguir hasta el infinito.
línea áurea
La razón entre el segmento entero y el segmento a es la misma que la razón entre los segmentos a y b, esta es la razón áurea.
(a+b)/a = a/b -> a² = b(a+b) = ba+b² -> a² - ba - b² = 0
Para averiguar el valor de a vamos a solucionar esta última ecuación de segundo grado.
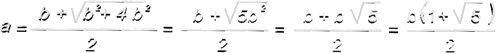
a/b = Φ -> 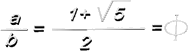
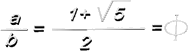
Como ha visto el arte tiene mucho que ver con las matemáticas y estas a su vez intentan dar explicaciones lógicas a la naturaleza y este universo tan grande y curioso.
Por lo tanto es lógico que el hombre utilice las matemáticas para representar a través del arte este universo que nos rodea.
También es lógico que empleemos herramientas basadas en las matemáticas para crear arte.
BIBLIOGRAFIA:
Muy bien la entrada
ResponderEliminar